学习笔记:平方根倒数与0x5f3759df
2023-09-26 12:09
我发现自己好不容易搞清楚的东西很快就会忘记,除非写个笔记下来,忘记了也许看看还能想起来。
本文是关于雷神之锤游戏代码中使用过的平方根倒数速算法(维基百科)的原理。尽管维基百科和一个流传很广的 youtube 视频已经解释得很清楚,我还是记录下来我当下的理解。
代码:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
这段代码可以快速求出输入值的平方根倒数(1/sqrt(x))的近似值。
原理:
这个算法使用了两个核心技巧。一是将浮点数按照整数的规则进行运算;二是利用函数 y = log_2(1+x) 在 0 到 1 区间内与函数 y = x 非常吻合的特性。
1,对浮点数进行整形运算

浮点数的表示方法本质上是二进制下的科学计数法。如上图 32 位 bit,最开始 1 bit 是正负号(在本算法中,因为是计算平方根,所以输入值永远为正);之后 8 bits 为指数部分(2 为底数);最后 23 bits 为有效数字的小数部分(这个二进制的有效数字可以写成形如 1.0100… 的形式,其中整数部分永远为 1,省略)。
然后,我们假设指数部分的值为 E;有效数字小数部分单独取出来、以整数的形式表示的值为 M。再尝试用 E 和 M 构建这个浮点数的值。
注意,M 是一个整数,如果要将它变回形如 0.0100… 的小数,需要除以 2^23。同时,E 是取值为 [0, 255] 的非负整数,需要减去 127 调整为取值 [-127, 128] 的整数。因此,原浮点数可以表示为:
(1 + M / 2^23) * 2^(E - 127)
1+M/2^23 构成有效数字 1.0100…,乘以 2 的 E-127 次方,这个科学计数法表示的数字就是这个浮点数的值。但是在储存这个浮点数的时候,我们只是取出 E 和 M 的部分,连同正负号拼成一个 32 位长度的二进制数去保存。
而如果我们不知道这个 32 位的二进制数字是浮点数,把它当作一个整数拿出来,它所代表的数字就完全不同了:
(E * 2^23 + M)
浮点数不同位上的数字有不同的含义,它显然不能按照整数的计算方法去操作。比如:对于整数,移位是一种常见的操作,右移一位是除以 2,左移一位是乘以 2。但是浮点数如果进行移位,其分别表示指数和小数的部分就错位了。这样的结果按说没有任何意义。但在这个特殊的速算法中,一个浮点数被强制解释成了整数,像整数一样进行了右移操作,然后与另一个整数相减。这样所得的值为什么正好是平方根倒数呢?这就需要进行以下推导:
2,获取近似值的数学推导
回到最初,假设输入值是 x,平方根倒数计算结果是 y,即:
y = 1 / sqrt(x)
可以写成指数的形式:
y = x^(-1/2)
两边求 log:
log_2(y) = log_2[x^(-1/2)]
log_2(y) = -1/2 * log_2(x)
由于 x 和 y 都是浮点数,设他们的 E 和 M 分别是 Ex、Mx、Ey、My。将上式写成浮点数表示方法:
log_2[(1 + My / 2^23) * 2^(Ey - 127)] = -1/2 * log_2[(1 + Mx / 2^23) * 2^(Ex - 127)]
根据 log 运算规则可进行如下变形:
log_2(1 + My / 2^23) + log_2[2^(Ey - 127)] = -1/2 * {log_2(1 + Mx / 2^23) + log_2[2^(Ex - 127)]}
log_2(1 + My / 2^23) + Ey - 127 = -1/2 * [log_2(1 + Mx / 2^23) + Ex - 127]
移项、合并同类项:
log_2(1 + My / 2^23) + Ey - 127 = -1/2 * log_2(1 + Mx / 2^23) - 1/2 * Ex + 1/2 * 127
log_2(1 + My / 2^23) + Ey = -1/2 * log_2(1 + Mx / 2^23) - 1/2 * Ex + 3/2 * 127
注意左右两边都有 log_2(1 + M / 2^23) 这样形式的项。而 M / 2^23 是有效数字的小数部分,也就是说它的取值范围是 [0, 1)。而我们看下图:
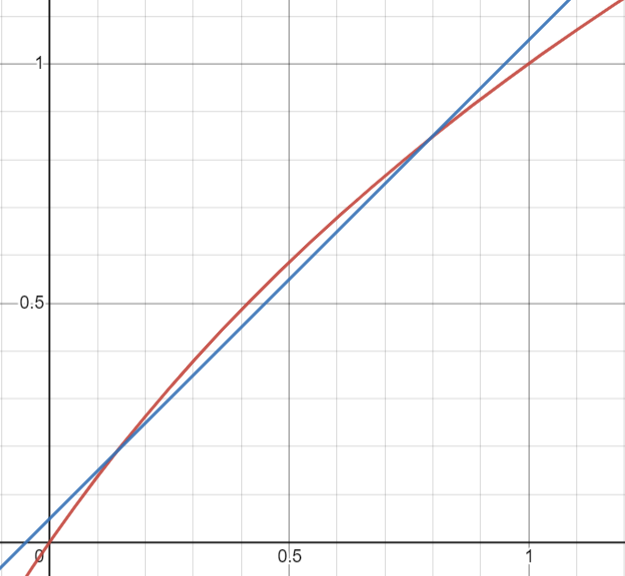
图中红色曲线为函数 y = log_2(1+x),它在 0 到 1 区间内与进行了稍许移位的函数 y = x(蓝色直线)非常吻合。也就是说,我们可以用 x + σ(σ 为一个很小的常数,其值待定)来近似地替换 log_2(1+x) 的值。进行替换后,上式变为:
My / 2^23 + σ + Ey = -1/2 * (Mx / 2^23 + σ) - 1/2 * Ex + 3/2 * 127
移项、合并同类项、各项乘以 2^23:
My / 2^23 + σ + Ey = -1/2 * (Mx / 2^23) - 1/2 * σ - 1/2 * Ex + 3/2 * 127
My / 2^23 + Ey = -1/2 * (Mx / 2^23) - 1/2 * Ex + 3/2 * 127 - 3/2 * σ
My / 2^23 + Ey = -1/2 * (Mx / 2^23 + Ex) + 3/2 * (127 - σ)
My + Ey * 2^23 = -1/2 * (Mx + Ex * 2^23) + 3/2 * (127 - σ) * 2^23
注意,原先作为浮点数组成部分的 E 和 M,此时此刻恰好符合整数的表达形式 (E * 2^23 + M)。也就是说,当我们将一个浮点数(设为float_x、float_y)强制看成一个整数(记作 int_x、int_y)去进行运算,则根据 float_y = 1 / sqrt(float_x) 可以推导出:
int_y = -1/2 * int_x + 3/2 * (127 - σ) * 2^23
这正是算法中 i = 0x5f3759df - ( i >> 1 ); 所进行的运算。其中常数 0x5f3759df 即为 3/2 * (127 - σ) * 2^23 的取值;右移一位即除以 2。这个整数运算所得的结果再强制变换回浮点数形式,就得到了 float_y 的近似值。
3,后续步骤
最后对近似值使用牛顿迭代法,进一步使其精确。牛顿迭代法是利用函数导数的性质、通过多次迭代近似地求解方程的方法。详见维基百科。