2D Fully Connected Layer:一种无用的对线性全连接层的模仿
2024-08-05 13:08
结论:我用另一种方法实现了pytorch的线性全连接层(torch.nn.Linear)。
与原本相比本质没有任何改变,性能没有提升,使用场景没有得到扩展。白折腾。
轻小说里叫纯白天使,我这叫纯白折腾。
简单说一下,game点是这样:
当线性层接受的数据是二维数组,比如灰度图像时,通常的做法是把数据拉平成一维。比如我们要处理手写数字识别的数据(MNIST),每一个数据是一个28x28的灰度图,类似这样:
我们创建一个最简单的线性层模型来识别这些数字,模型是这样的:
model_1_linear = nn.Linear(28 * 28, 10).to(device)
那么在训练的时候,我们就需要将维度为28x28的二维数组转变成长度为28 * 28 = 784的一维数组。
for x, y in train_loader:
x = x.view(-1, 28 * 28).to(device)
y = y.to(device)
这里batch_size为200。x变换之前是200x28x28,经过x.view(-1, 28 * 28)之后就是200x784。模型的权重参数weight的维度是784x10,二者点乘运算的结果就是我们需要的维度200x10。
这个时候一个idea就出现了:你将二维图像数据拉平,那不是破坏了图像的原始结构了吗?如果你保持二维数据的维度,再搞一个更高维度的权重参数参与计算,会不会更容易体现出像素点之间的空间联系,得到更好的训练效果呢?
于是我就写出了第一版的2D Fully Connected Layer:
class TwoDFC(nn.Module):
def __init__(self, input_size, output_size):
super(TwoDFC, self).__init__()
self.weight = nn.Parameter(torch.randn(1, *input_size, output_size))
def forward(self, x):
# x.shape == (batch_size, *input_size)
x = x.unsqueeze(-1)
product = x * self.weight
return product.sum(dim=(1, 2))
model_2d_fc = TwoDFC((28, 28), 10).to(device)
计算过程是这样的:数据进来时的维度是200x28x28;经过x.unsqueeze(-1)变成200x28x28x1方便后续计算;然后x与维度为28x28x10的weight进行星号乘法,也就是在28x28的维度上各元素按位相乘,在x10的维度上广播,结果的维度为200x28x28x10;最后,对28x28的维度进行求和,这两个维度消失了,最终就得到了200x10的结果矩阵。
写完我还挺得意的,这么复杂算出来的效果应该比原来一维的线性模型表现更好吧?
然后半夜我从床上坐起来:“不是,我有病吧?”
这不就是一维线性模型吗?计算过程是一毛一样的啊!784个元素分别相乘再求和。
最可气的是我训练了一下,效果比原版的线性层差远了!
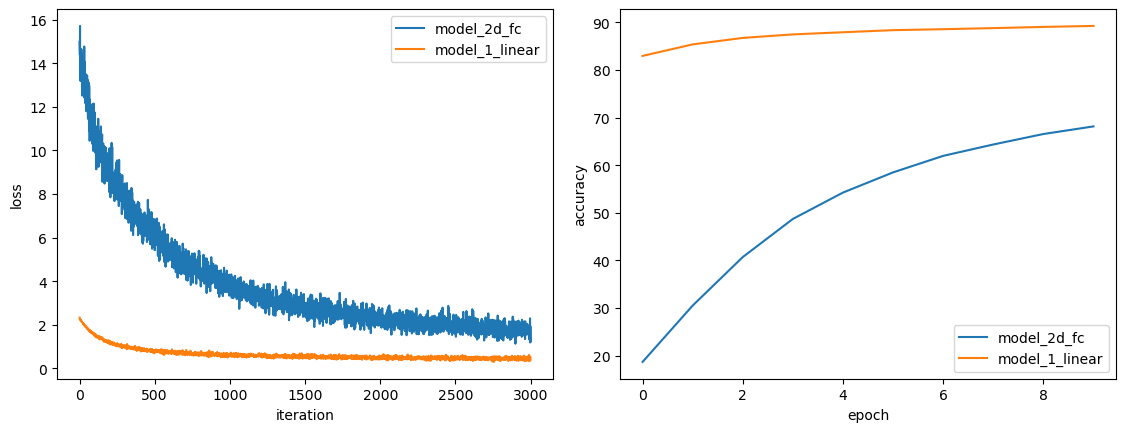
(optimizer: torch.optim.SGD; learning rate: 0.01; training data size: 60000; validation data size: 10000; epochs: 10)
我想既然开始做了,半途而废不好,至少给它升升番。再说既然它和线性层有相同的计算过程,那么效果也不应该差这么多才对。
仔细一看,是我忘了加bias。于是加上成了第二版:
class TwoDFCv2(nn.Module):
def __init__(self, input_size, output_size):
super(TwoDFCv2, self).__init__()
self.weight = nn.Parameter(torch.randn(1, *input_size, output_size))
self.bias = nn.Parameter(torch.randn(output_size))
def forward(self, x):
# x.shape == (batch_size, *input_size)
x = x.unsqueeze(-1)
product = x * self.weight
return product.sum(dim=(1, 2)) + self.bias
训练完一看,也没有好很多:
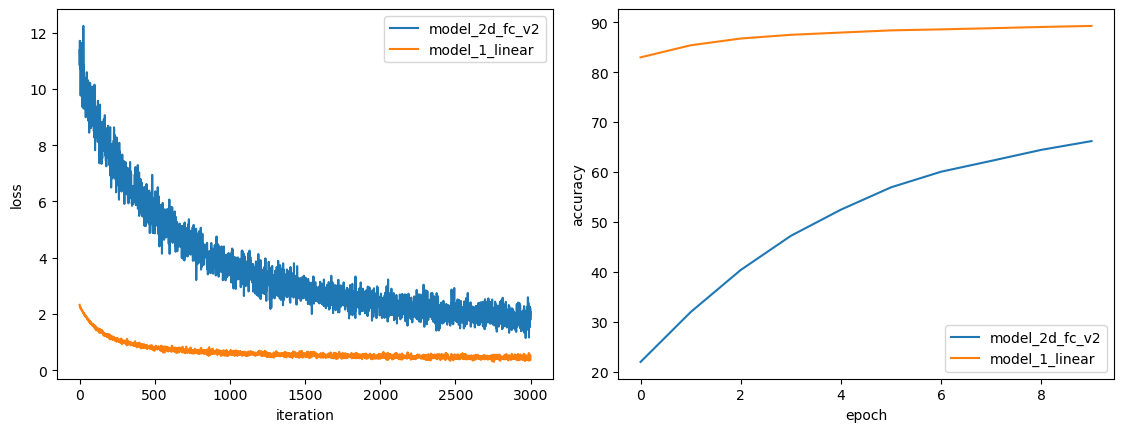
这时的模型参数量和线性层是完全一样的,训练参数也一样。从曲线上看是初始的时候和线性层差别最大,怀疑是权重参数初始化的问题。看了一下torch.nn.Linear源代码的参数初始化过程,复制粘贴过来,成了第三版:
class TwoDFCv3(nn.Module):
def __init__(self, input_size, output_size):
super(TwoDFCv3, self).__init__()
self.weight = nn.Parameter(torch.randn(1, *input_size, output_size))
self.bias = nn.Parameter(torch.randn(output_size))
self.fan_in = np.prod(input_size)
self.reset_parameters()
def reset_parameters(self):
a = np.sqrt(5.)
gain = np.sqrt(2.0 / (1 + a ** 2))
std = gain / np.sqrt(self.fan_in)
bound = np.sqrt(3.0) * std
with torch.no_grad():
self.weight.uniform_(-bound, bound)
bound1 = 1 / np.sqrt(self.fan_in)
with torch.no_grad():
self.bias.uniform_(-bound1, bound1)
def forward(self, x):
# x.shape == (batch_size, *input_size)
x = x.unsqueeze(-1)
product = x * self.weight
return product.sum(dim=(1, 2)) + self.bias
很神奇,这回和线性层不相伯仲,不分彼此:
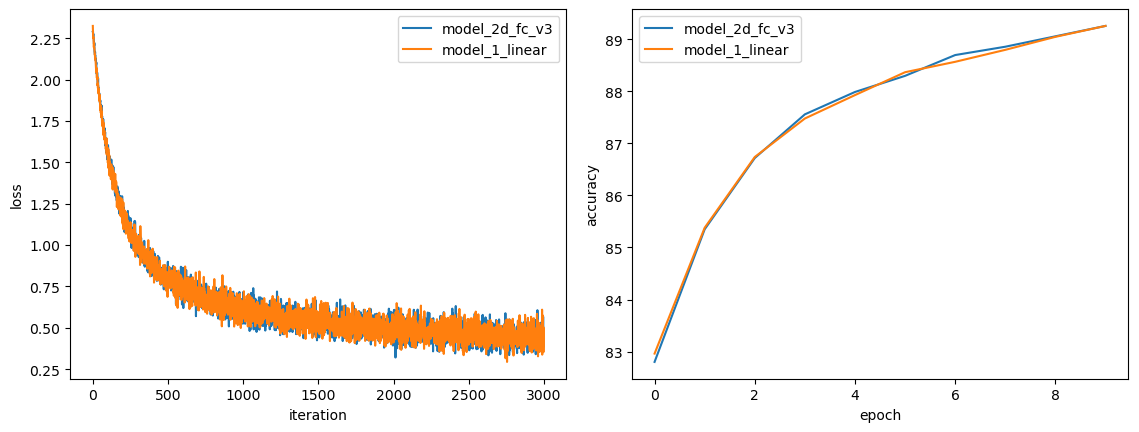
所以,我证明了:两个参数完全相同、初始化过程一致、计算本质一模一样的模型,使用同一组数据进行同样的训练,结果能够完美地拟合。
(您别挨骂了!)